手机扫一扫服务随身走
或在手机浏览器中输入
www.hnfudu.com
导读：
2025年高考数学考试结束后，考场外的考生们神情各异：有人低头沉默，有人掩面叹息，有人甚至红着眼眶走出考场。社交平台上，“数学太难了”“今年卷王还是22届”等话题迅速冲上热搜。
没有人会一直破防除非22届考生怎么回事
今年高考期间，“22届没惹”成为热梗。这一网络用语暗指“2022届考生无辜被卷”，却因当年考试难度成为全网“破防”的代名词。
当2022届考生看到这些讨论时，却只能苦笑一声：“别提了，我们才是真正的‘破防之王’！”
破防之源：2022年高考的“地狱级难度”
1、被载入史册的逆天考题
语文作文题要求结合“本手、妙手、俗手”三类围棋术语，联系生活实际展开论述。题目本身晦涩难懂，而材料背景又涉及《红楼梦》中“亭台题名”的典故，被网友戏称“曹雪芹来了都要复读”。
考生直呼“题目读完已崩溃”。对比2024年直白务实的作文题（如互联网与人工智能议题），22届考生在评论区集体呐喊：“我们写《红楼梦》时连题干都看不懂！”
2、数学：平均分创历史新低
2022年数学卷的难度堪称“教科书级灾难”。选择题中，一道“垃圾分类”应用题让无数考生抓耳挠腮；大题部分，压轴题“圆锥曲线+概率统计”组合拳直接击溃学生信心。
数据显示，当年数学平均分较往年下降超20%，许多中等生因数学失利被迫进入大专。有考生回忆：“考场上两个小时，我只写了半小时，剩下的时间都在蒙题。”
3、分数线的残酷暴击
23届高考难度下调后，多省分数线大幅上涨。湖南等地考生晒出对比图：同样努力，22届分数竟比23届低30分以上，直接导致志愿滑档。“我们熬最深的夜，挨最毒的打！”成22届考生通用签名。
二、就业寒冬更是雪上加霜
熬过了高考的艰难，22届考生以为人生迎来了新的曙光，然而，当他们在 2022 年毕业时，又遭遇了就业的寒冬，这无疑是雪上加霜。
2022年，高校毕业生人数达到了1076万，规模和增量均创历史新高。如此庞大的毕业生群体涌入就业市场，使得竞争异常激烈。
在招聘会上，常常是人潮涌动，一份热门岗位往往收到成百上千份简历，毕业生们为了一个机会争得头破血流。
就业市场的竞争激烈还体现在学历内卷上。随着毕业生数量的增加，企业的招聘门槛也水涨船高。很多企业在招聘时，优先考虑 985、211 高校的毕业生，甚至一些非双一流院校的毕业生连简历筛选这一关都难以通过。
22届考生被认为是最惨的一届，主要原因包括高考和就业方面的巨大挑战。
高考难度大且分数线高
2022年高考被称为“地狱级难度”，具体表现在以下几个方面：
语文作文题晦涩难懂：作文题要求结合“本手、妙手、俗手”三类围棋术语，联系生活实际展开论述，题目本身晦涩难懂，涉及《红楼梦》中“亭台题名”的典故，被网友戏称为“曹雪芹来了都要复读”。
数学卷难度大：数学卷的难度堪称“教科书级灾难”，选择题中的“垃圾分类”应用题让考生抓耳挠腮，大题部分的压轴题“圆锥曲线+概率统计”组合拳直接击溃了学生信心，当年数学平均分较往年下降超20%。
分数线高：23届高考难度下调后，多省分数线大幅上涨，导致22届考生的分数相对较低，许多考生因此未能进入理想的大学。
就业市场严峻
2022届毕业生在就业市场上也面临巨大挑战：
毕业生数量多：2022年高校毕业生人数达到1076万，规模和增量均创历史新高，使得就业市场竞争异常激烈。
就业难：7月份16-24岁城镇青年人失业率为19.9%，经济下行和疫情反复导致企业招聘减少，许多毕业生面临就业困难。
企业招聘门槛高：随着毕业生数量的增加，企业的招聘门槛也水涨船高，许多岗位要求985、211高校毕业生，甚至一些非双一流院校的毕业生难以找到工作
（网络收集）2025年全国二卷数学高考真题文字版
2,8,14,16,20平均数为
A.
B.
C.
D.
2. 
，
A.
B.
C.
D.
3. 
，
，
A.
B.
C.
D.
4. 
解集是
A.
B.
C. 
D.
5. 
，
，
，
，
A.
B.
C.
D.
6. 抛物线
焦点
，
，过
作
准线的垂线，垂足为
。若
，则
A.
B.
C.
D.
7. 
为等差数列
前
项和，
，
，
A.
B.
C.
D.
8. 
，
，
A.
B.
C.
D.
9. 为等比数列前项和，
为公比
，则
A.
B.
C.
D.
10. 
定义在
上奇函数，x＞0时，
，则
A.
B. 当x＜0时，
C.
当且仅当
D.
是极大值点
11. 双曲线
左、右焦点为
，左、右顶点为
。以
为直径的圆与的一条渐近线交于
，且
，则
A.
B.
C.离心率为
D. 当
时，四边形
面积为
12.
，
，
，则
____
13.
是
极值点，则
____
14.一个底面半径为
，高为
的封闭圆柱形容器，内有两个半径相等的铁球，则铁球半径的最大值为____
。
15.
，
(1) 求
。
(2)
，求
值域和单调区间。
16.椭圆
的离心率为
，长轴长为
。
(1) 求
的方程。
(2) 过点
的直线
与交于
，
为坐标原点，若
，求
。
17.如图，四边形
中，
，
，
为
中点，
在
上，
，
，
。将四边形
沿
翻折至四边形
，使得面
与面
所成的二面角为
。
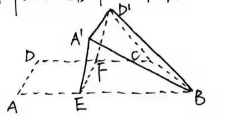
(1) 证明：
平面
。
(2) 求面
与面所成二面角的正弦值。
18.
，
。
(1) 证明：
在
存在唯一极值点和唯一零点。
(2) 设
为在的极值点和零点。
(i)
，证明：
在
单减
(ii) 比较
与
的大小，并证明。
19.甲、乙乒乓球练习，每个球胜者得
分，负者得
分，设每个球甲胜概率为
（
），乙胜概率为
，
，且各球胜负独立。对正整数
，记
为打完
个球后甲比乙至少多得
分的概率，
为打完个球后乙比甲至少多得分的概率。
(1) 求
（用表示）。
(2) 若
，求。
(3) 证明：对任意正整数
，
。(2)求面
与面
所成二面角的正弦值.
翻页
声明：该作品系作者结合法律法规，政府官网及互联网相关知识整合，如若内容错误欢迎联系我们修正。
相关知识推荐
岳阳市用户7分19秒前提交了需求
益阳市用户5分58秒前提交了需求
湘潭市用户9分35秒前提交了需求
株洲市用户4分15秒前提交了需求
株洲市用户8分28秒前提交了需求
招生老师
相关栏目
